© ULB- PhysGenLabs
with the collaboration of
Jean-Marie Frère
Paul Duhamel
Anastase Karusho
|
||||||
While "start at rest" is easily covered by normal video, there are several circumstances where a faster take proves useful.
I just chose 3
- Parabolic fall with a non-negligeable initial speed
(here, the speed can be determined independently from
the set-up, a ball rolling ON a U-shaped rail)
- Collision (balistic pendulum) : the advantage here is not so much in the speed, but in having an abundance of data to calculate the speeds at impact time, and check conservation of momentum -- simple pendulums are used, without the need of air tracks or tables
- Air friction on a sphere: this is a notoriously
difficult part. To measure a significant drag, a high
speed is needed (even to differentiate a ping-pong ball
from a steel bearing!) -- here about 5m/s
I have used version 4.62 on Windows64
and thank its author, Douglas Brown for friendly assistance
YOU NEED IT (if only to see the data from this page),
Is is freely available from:
http://www.cabrillo.edu/~dbrown/tracker/
Conservation of momentum
reminder: Download BOTH the video clip AND the Tracker file in the SAME directory, and open the tracker file from the Tracker program
Ball A (at rest) is hit by ball B,
With respective masses 95.7g and 57.1g, we measure the initial (horizontal) speed of B to be 64cm/s, and its (recoil, counted negatively) speed -16.6cm/s, while the recoil speed of A is 47cm/s.
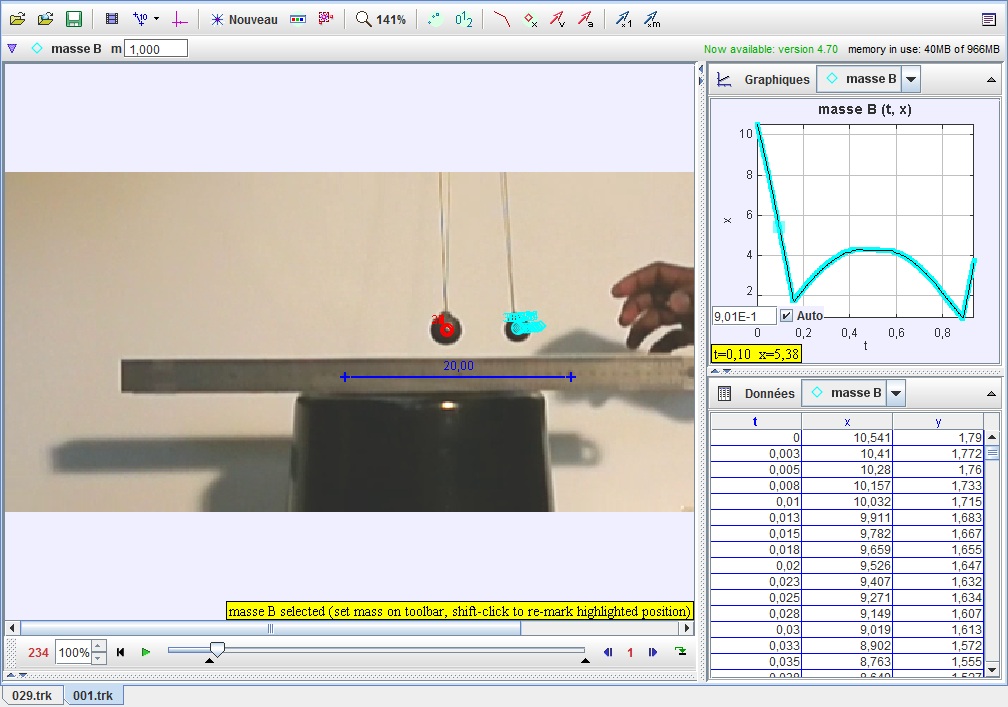
The balance of initial (3654 g cm/s) and final ( 3650 g cm/s ) momenta is well verified (accuracy of the measurement is a few percent, so the last digits should not be taken seriously in any case)
Here is the "Tracker file"
And the Video Clip
(this is the full clip, the best is to save both tracker file and video in the same folder, and open the tracker file in Tracker)
reminder: Download BOTH the video clip AND the Tracker file in the SAME directory, and open the tracker file from the Tracker program
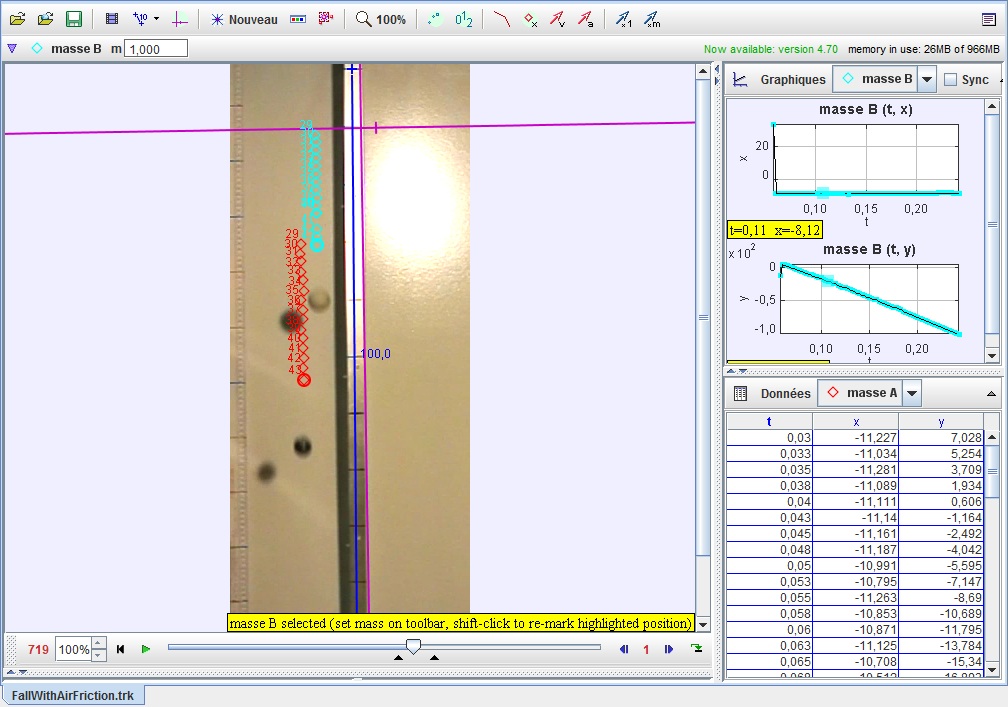
The video is taken where a speed of approx. 5m/s is reached.
It is easy to see that the table tennis ball "loses ground" (the entrance time is not significant, but the increase in distance between the balls is).
We did not try to fit the full trajectory to standard formula, as the trajectory is still very well described with a parabolic motion over the interval.
While the friction appears negligeable for the steel ball (acceleration = 9.8 m/s2), the friction is very visible on the table tennis ball with the (average over the path measured) a=5.42m/s2
(again, accuracy is only a few percent, but I did not round up the last digits).
This allows to measure the ratio of friction force (Ff) to mass for the second projectile : Ff/m = 4.36 m/s2
The friction force is found to be in good agree
(see for instance : http://en.wikipedia.org/wiki/Free_fall)
The Tracker File is found here
The Video File is found here :
reminder: Download BOTH the video clip AND the Tracker file in the SAME directory, and open the tracker file from the Tracker program
 asy
to calculate form the set-up: a sphere rolling ON a
U-shaped rail .. gives the students a bit to figure
out...). The advantage here is to have direct access (by
the slope) to the initial parameters of the fall, thanks
to the large number of points (thks for the
auto-tracking facility in the software! It is essential
in the present context)
asy
to calculate form the set-up: a sphere rolling ON a
U-shaped rail .. gives the students a bit to figure
out...). The advantage here is to have direct access (by
the slope) to the initial parameters of the fall, thanks
to the large number of points (thks for the
auto-tracking facility in the software! It is essential
in the present context) The Tracker File
The Video file
(other data were taken at 60fps with higher resolution but are not presented here; the price to pay for the 400 fps is a smaller frame - letter-box shaped)
Hint: don't forget to adjust the video speed in Tracker.
We found the 400 fps specification to be quite accurate
(filming a digital chronometer!)