Barre résonante
|
||||||
François
GONZE
ULB
Agrégation Sciences Physiques
Juin 2009
ULB
Agrégation Sciences Physiques
Juin 2009

Cette
expérience spectaculaire illustre les notions d'onde, d'onde
acoustique,
d'onde stationnaire, de fréquences harmoniques.
La mesure de la
fréquence émise par la barre permet de
calculer une valeur approchée de la vitesse de propagation d'une
onde acoustique longitudinale dans un barreau d'aluminium.
La mesure de la fréquence émise par la barre est effectuée à l'aide du logiciel Audacity.
Le barreau doit
impérativement être tenu en un noeud de
vibration sous peine de ne
produire aucun son persistant. A titre d'exemple, si le barreau est
maintenu au quart de sa longueur, c'est la deuxième harmonique
qui est émise.
Le frottement des
doigts enduits de colophane sur le barreau produit des vibrations
longitudinales qui se propagent dans le barreau. Arrivées aux
extrémités, les ondes sont réfléchies, ce
qui donnent lieu à des interférences au sein du barreau.
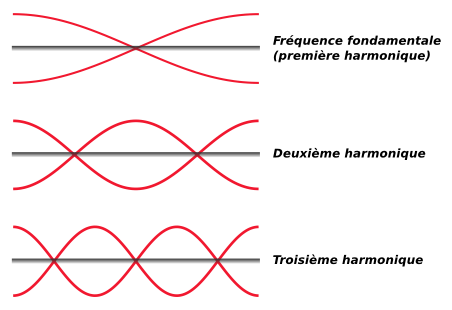
Les ondes stationnaires résonantes qui se
produisent présentent des ventres de vibration
aux extrémités du barreau car celles-ci sont libres de
vibrer. La fréquence la plus basse est appelée
fréquence fondamentale (ou première harmonique) tandis
que les fréquences supérieures sont appelées
fréquences harmoniques.
Les
extrémités du barreau mettent en vibration les
molécules d'air environnantes. Les vibrations longitudinales des
molécules d'air sont interprétées par notre
cerveau comme un son. La hauteur du son (la note jouée) est
déterminée par la fréquence de la vibration.
Au sein du barreau, la vitesse de propagation, la longueur d'onde et la fréquence sont liées par l'équation suivante :
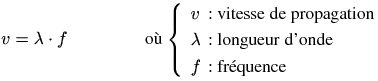
La distance entre deux ventres
consécutifs étant égale à la moitié
de la
longueur d'onde, les longueurs d'onde des ondes stationnaires
résonantes sont
telles que la longueur (fixe) L de la barre est un multiple entier de
la demi-longueur d'onde :
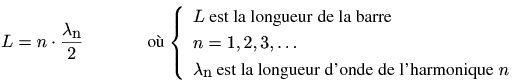
L'équation suivante montre que les
fréquences des harmoniques sont les
multiples entiers de la fréquence fondamentale :
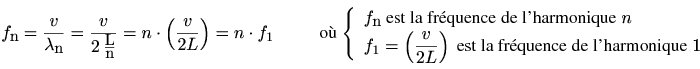
Au sein du barreau, la vitesse de propagation, la longueur d'onde et la fréquence sont liées par l'équation suivante :
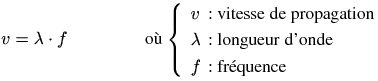
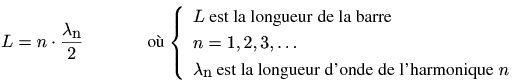
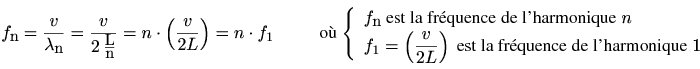
Le logiciel Audacity
permet d'enregistrer le son émis par le barreau et d'obtenir son
spectre (menu Analyse) de
fréquences.
 |
 |
 |
| Fréquence fondamentale | Seconde harmonique | Séquence
vidéo (Real player) |
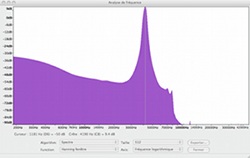
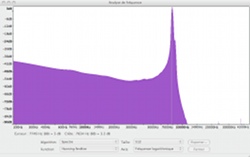
Lorsque le barreau
est maintenu en son milieu, la fréquence mesurée est 4190 Hz.
La fréquence
4190 Hz est la fréquence fondamentale. La fréquence 8378
Hz est très proche du double de la fréquence fondamentale
dont la valeur est 8380 Hz.
La longueur du barreau est égale à 60,8 cm. La vitesse de propagation de l'onde dans le barreau, calculée sur base de la fréquence fondamentale, est :
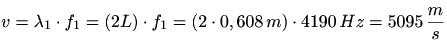
La masse (m), le diamètre (D) - dont on déduit le rayon (R) - et la longueur (L) de la barre ont les valeurs suivantes :
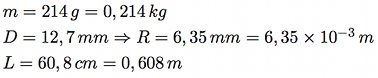
NB : Le diamètre du barreau a été mesuré à l'aide d'un pied à coulisse.
Ces données permettent de calculer la masse volumique du barreau :
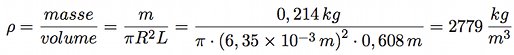
La masse volumique et le module de Young (Y) de l'aluminium renseignés dans le livre University Physics (pp 416 et 516 - voir références ci-dessous) ont les valeurs suivantes :
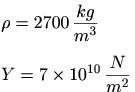
La longueur du barreau est égale à 60,8 cm. La vitesse de propagation de l'onde dans le barreau, calculée sur base de la fréquence fondamentale, est :
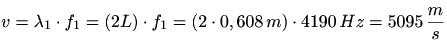
La masse (m), le diamètre (D) - dont on déduit le rayon (R) - et la longueur (L) de la barre ont les valeurs suivantes :
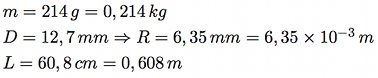
NB : Le diamètre du barreau a été mesuré à l'aide d'un pied à coulisse.
Ces données permettent de calculer la masse volumique du barreau :
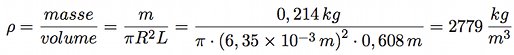
La masse volumique et le module de Young (Y) de l'aluminium renseignés dans le livre University Physics (pp 416 et 516 - voir références ci-dessous) ont les valeurs suivantes :
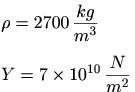
L'expression
théorique de la vitesse de propagation d'une onde longitudinale
dans un barreau est (University Physics p 599) :
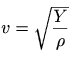
Cette équation fournit la valeur suivante pour
la vitesse de propagation :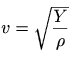
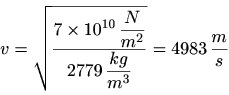
La fréquence fondamentale déduite de cette vitesse a la valeur suivante :
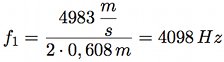
Nous constatons un
accord évident (aux incertitudes de mesure près) entre
les valeurs expérimentales et les valeurs fournies par la
théorie.
La barre en
aluminium
et la colophane (rosin en
anglais) peuvent être achetées chez diverses
sociétés (rechercher singing
rod via Google).
Le logiciel Audacity
peut être
téléchargé gratuitement (faire également
une recherche via Google).
 |
 |
Young & Freedman
International Edition
Pearson Addison Wesley