L'Energie, des jeux de cubes aux antiparticules.
|
|
|
La conservation de l'énergie : découverte ou invention ?
Nous
commencerons par une question un peu philosophique : « que signifie la conservation
de l'énergie ? » Plus précisément, devons-nous y voir une « loi de la Nature »,
préexistante, que nous avons eu la perspicacité de découvrir, ou plutôt une
pure création humaine, qui nous permet simplement d'appréhender notre environnement
sous une forme traitable par notre cerveau ?
La
question est évidemment plus générale que la notion d'énergie, et s'applique
à l'ensemble des « lois physiques ». Nous ne prétendons pas la résoudre ici.
L'image
de lois « préexistantes » est souvent confortée par l'idée d'une description
mathématique universelle, indépendante des applications, mais je crois que
c'est à tort que l'on en tirerait argument. L'on sait en effet combien la
description des lois physiques a contribué au développement des mathématiques,
ce qui ne fait que reporter une étape plus loin la question de départ.
|
The Feynman lectures on physics,
vol. I, début du chapitre 4. |
J'aimerais
au contraire reprendre ici une image que je trouve très parlante de la notion
de conservation d'énergie. On en trouvera une description à la fois amusante
et détaillée dans le très célèbre cours de Richard Feynman; je me contenterai
de paraphraser ici l'argument.
|
Cliquez sur l'image pour l'agrandir

R.Feynman |
Feynman
évoque une comparaison avec une maman qui, chaque soir, range le jeu de cubes
de son jeune enfant. Les cubes sont identiques, indestructibles, et elle
en compte toujours le même nombre. Ceci la conduit à formuler la loi :
Le nombre de cubes est constant dans le temps.
Un
jour toutefois elle constate que des cubes manquent, mais les aperçoit dans
le jardin, sans doute lancés là par la fenêtre ouverte. Les ayant récupérés,
elle formule sa loi de façon plus précise :
Si toutes les fenêtres restent fermées,
le nombre de cubes est constant.
Mais
voici qu'un soir plusieurs cubes ont disparu, tandis que l'enfant refuse
obstinément d'ouvrir sa boîte à trésors. Avec un peu d'ingéniosité, la maman
pèse un cube, et ne tarde pas à établir une nouvelle loi, plus générale :
Si toutes les fenêtres restent fermées,
le nombre de cubes,
additionné de l'accroissement de la masse de la boîte à trésor,
divisé par la masse d'un cube, est constant.
Elle trouve d'ailleurs plus commode d'utiliser la formulation suivante :
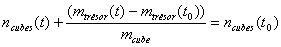 |
(1) |
où m trésor(t0) est naturellement la masse de la boîte à trésors au début de l'expérience, quand elle ne contenait aucun cube.
Le
récit de Feynman se poursuit : fenêtres toujours fermées, un beau soir, l'équation
ci-dessus n'est plus satisfaite... mais la maman remarque que le niveau de
l'eau de la baignoire est un peu plus élevé que d'ordinaire après le débarbouillage
de son rejeton ; l'eau est fort sale, et elle ne peut en apercevoir le fond
mais, mesurant le volume d'un cube, elle complète son équation :
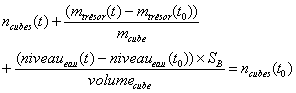 |
(2) |
où SB représente la surface de la baignoire.
Nous
laisserons au lecteur la fantaisie d'imaginer d'autres péripéties -qui l'amèneront
à ajouter des termes à la somme- mais, par souci de commodité, nous ré-écrivons
maintenant cette équation sous une forme à peine différente (les quelques
points sont laissés à l'imagination du lecteur) :
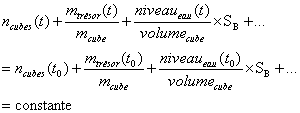 |
(3) |
L'exemple
choisi par Feynman est bien sûr ludique, mais l'on pourrait en tirer une
série d'enseignements. Nous réserverons la remarque la plus importante de
Feynman pour la fin.
Le plus évident, c'est la recherche d'une loi de conservation :
le souci de définir à travers toutes ces péripéties une quantité qui ne varie
pas dans le temps, même si cela implique de compliquer considérablement la
définition de cette quantité. Nous ne nous interrogerons pas davantage sur
les raisons psychologiques ou autres de rechercher une telle loi de conservation ;
de façon purement pragmatique, le fait qu'une quantité soit constante simplifie
souvent la résolution d'un problème physique.
Par
ailleurs, même à ce niveau de raisonnement élémentaire, on peut observer
la commodité d'une formulation « mathématique » : sans cela, les énoncés
deviennent vite lourds et peu commodes à manipuler. Le choix de cette notation
est déjà la recherche d'une adéquation du formalisme au mode de traitement
le plus efficace.
Cette allégorie se compare évidemment à la conservation de l'énergie tout est effectivement transposable, la conservation de l'énergie d'un système isolé
(correspondant aux fenêtres fermées) consiste aussi dans la constance d'une
somme comprenant des termes assez hétéroclites, ajoutés au fil du temps pour
pallier à des manquements de la formulation initiale. On y trouve pêle-mêle
l'énergie cinétique -des carrés de vitesses (chers aux émissions de sécurité routière)- et l'énergie potentielle,
qui peut revêtir des formes très variées, liées à la hauteur d'un objet ou
à l'extension d'un élastique. On y rencontre aussi peut-être le carré d'un
champ électrique ou magnétique, voire la température d'un solide ou d'un
liquide, la pression d'un gaz, la masse d'un noyau, un nombre de particules
émises ou absorbées,...
Mais la remarque la plus importante de Feynman est sans doute la dernière qu'il ait formulée : dans l'analogie avec la conservation de l'énergie, on ne retrouve pas l'équivalent... des blocs !
Et
c'est fondamental car, dans le raisonnement précédent, nous avons admis au
départ l'existence d'un objet matériel indestructible, qui justifiait toute
la démarche et l'introduction des termes successifs, tandis que, dans le
contexte de l'énergie, nous ne possédons que la somme de termes hétéroclites
analogues aux différentes fractions de notre équation.
L'énergie
est donc une notion bien plus abstraite que ne le suggérait l'exemple choisi,
et rien (sinon peut-être l'existence même d'une loi de conservation) ne laisse
supposer qu'une telle notion soit pré-existante à notre démarche.
La
conservation de l'énergie : loi de la Nature découverte par les scientifiques
avec une précision croissante à travers les âges ou invention de notre esprit
pour lui permettre d'appréhender le monde, ajustée (rafistolée ?) à chaque
étape ? Je m'abstiendrai de trancher, laissant au lecteur le soin de se forger une opinion.
Peut-être
n'est-ce aussi qu'une fausse question... Il serait intéressant d'approcher
une autre démarche conduisant aux lois de conservation. En effet, une formulation
moderne de la physique associe étroitement les principes de conservation
à la présence d'invariances d'un système sous diverses transformations. Par
exemple, la conservation de la quantité de mouvement est ainsi étroitement liée à l'invariance de translation (il n'y a pas d'origine privilégiée), et la conservation de l'énergie aux translations temporelles
(le système ne connaît pas d'instant privilégié). Les principes de conservation
ne sont alors que le reflet logique de ces hypothèses (ou de ces idéalisations).
|
|
La
démonstration est simple, et ne demande pas de mathématiques au-delà de celles
enseignées dans le secondaire ; qu'il suffise ici de préciser que, comme
les concepts d'espace et de temps sont unifiés en théorie relativiste (conduisant
à des vecteurs à 3 + 1 composantes, (r, ct)), la même unification lie la quantité de mouvement (p=mv) et l'énergie pour former le vecteur (p, E/c).
Comme la définition de la quantité de mouvement dans un référentiel donné
ne comprend pas de constante arbitraire, l'énergie qui y est associée est
elle aussi définie de manière unique. Remarque : conformément à la notation
usuelle, c représente ici la vitesse de la lumière dans le vide.
|
Relativité et énergie
L'avènement de la relativité restreinte a apporté une surprise dans la définition de l'énergie.
Si
nous prenons l'exemple de l'équation (3) ci-dessus, et que nous l'adaptons
à l'expression de l'énergie d'une particule neutre, isolée, nous obtenons
quelque chose du style :
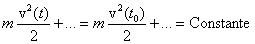 |
(4) |
où
nous avons simplement explicité le terme d'énergie cinétique. Mais nous sommes
bien évidemment libres d'ajouter n'importe quel terme constant à chacun des
membres de l'équation. En effet, en théorie non relativiste, l'énergie, même d'une particule libre, n'est définie « qu'à une constante arbitraire près ».
Il n'en va pas de même dans une approche relativiste, même si nous n'en donnons pas ici la démonstration (voir remarque ci-contre). On trouve en fait l'expression unique :
 |
(5) |
|
On trouvera dans l'intéressante brochure de R. Carreras:
« Et l'énergie devint matière »,
diffusée par le CERN,
une présentation illustrée de ce domaine de la physique
|
Dans
cette équation, c représente la vitesse de la lumière dans le vide, et le
membre de droite est une approximation valable dans la limite où les vitesses
v sont nettement inférieures à la vitesse de la lumière. On retrouve bien
l'expression familière de l'énergie cinétique, mais on constate aussi que
la constante est maintenant fixée de manière unique et qu'elle dépend de
la masse de la particule.
L'histoire
de ce terme est bien connue, puisqu'elle est à l'origine des développements
de la physique nucléaire d'abord, de la physique des particules ensuite.
Il montre que la masse des particules fait partie du bilan d'énergie, mais
on en déduit aussi que cette énergie peut être libérée par désintégration
de la particule. A l'inverse, la concentration d'une quantité d'énergie suffisante
dans un très petit volume (comme lorsque des particules légères mais de haute
énergie sont lancées les unes contre les autres à l'aide d'un accélérateur)
peut créer des particules plus lourdes. A titre d'exemple, l'accélérateur
LEP au CERN réalise le choc d'un électron et d'un antiélectron pour créer
des particules (comme le boson intermédiaire Z) de masse près de 100.000
fois plus élevée que celle des particules initiales !
|
Ce
problème ne se poserait pas de la même manière en théorie non relativiste,
où le zéro d'énergie est purement conventionnel ; la question de la stabilité
du système se poserait toutefois.
|
Energie du vide et mécanique quantique
Il n'est peut-être pas inutile d'évoquer ici la situation de la mécanique quantique.
L'une des hypothèses de base en est que l'on ne peut mesurer simultanément,
avec une précision arbitrairement élevée, la position et la vitesse d'une
même particule.
Cela
veut dire que, si je spécifie de façon absolument précise la position d'une
particule, je perds toute information sur sa vitesse et réciproquement. Envisageons
maintenant l'image d'un petit oscillateur, c'est-à-dire par exemple d'une
particule retenue par un ressort, dont nous négligerons la masse, et réfléchissons
à ce que cette situation implique pour la description de l'énergie.
Puis-je
placer ma particule dans un état d'énergie nulle ? Si je spécifie la position
« de repos », je ne connais plus la vitesse, et donc l'énergie cinétique :
je ne pourrais donc certainement pas affirmer qu'elle est nulle. Par contre,
si je précise une énergie cinétique (et donc une vitesse) nulle, je perds
toute information sur la position, à laquelle est associée l'énergie potentielle
due au rappel du ressort. Il en résulte que, même dans son état « de repos »,
cet oscillateur (la particule attachée à son ressort) doit posséder une énergie
non nulle. On montre en effet que les niveaux énergétiques successifs d'un
oscillateur, dans le traitement quantique sont :
 |
(6) |
où n
représente la fréquence de résonance de l'oscillateur. On constate donc que,
en-dehors des excitations successives caractérisées par des niveaux d'énergie
bien séparés, correspondant à l'émission ou l'absorption d'un quantum, figure
un terme constant, présent même en l'absence d'excitation (hn/2) : il s'agit de l' « énergie de repos ».
Son
importance apparaît pleinement en théorie quantique relativiste, et plus
spécialement en « théorie quantique des champs » où la description des particules
élémentaires se ramène au traitement de tels oscillateurs.
L'état
d'énergie le plus bas d'un système quantique est communément appelé « vide ».
Il en résulte que ce vide, état d'énergie minimum, comporte quand même une
certaine densité d'énergie, dont l'importance apparaît d'ailleurs dans les
traitements cosmologiques.
Energie négative ou antiparticules ?
Le
sujet surgit un peu sous la plume, car il m'est difficile de mentionner côte
à côte la mécanique quantique et la relativité restreinte sans évoquer l'une
des conséquences importantes de leur unification. En effet, lorsqu'on vient
à formuler une mécanique quantique relativiste, on sait que le temps et la
position doivent être traités sur le même pied, et l'on peut montrer qu'il
en va de même de l'énergie et de la vitesse ou, plus exactement, de la quantité
de mouvement mv.
Lorsque
l'on écrit de telles équations, ce n'est pas l'équation (5) ci-dessus qui
apparaît directement, mais plutôt son carré, et il en résulte deux solutions :
l'une positive, l'autre négative. Comme l'énergie relativiste est définie
sans l'ambiguïté d'une constante (voir remarque ci-contre), nous n'avons
pas choix de redéfinir le zéro d'énergie, et nous devons bien faire face
à une quantité d'énergie négative. C'est le formalisme de la théorie quantique
des champs qui y apporte cette fois réponse. Une telle théorie doit en effet
rendre compte de la possibilité de créer et détruire des particules et, plutôt
que de décrire les particules elles-mêmes, elle formule les équations pour
les opérateurs de création et de destruction de particules. Une ré-interprétation
simple se présente alors : sans modifier le bilan énergétique du système,
on peut substituer les notions comme suit, au niveau de ces opérateurs :
|
| Création d'une particule d'énergie -w |
« |
Destruction d'une antiparticule d'énergie +w |
|
Destruction d'une particule d'énergie -w |
« |
Création d'une antiparticule d'énergie +w |
|
Cliquez sur l'image pour l'agrandir
 P.A.M. Dirac P.A.M. Dirac |
Cette conséquence simple de l'association de la mécanique quantique et de la relativité restreinte conduisit ainsi Dirac à postuler l'existence d'antiparticules,
possédant exactement la même masse, mais des charges (par exemple électrique)
opposées aux particules correspondantes. Leur découverte, d'abord dans le
rayonnement cosmique car on ne disposait pas d'accélérateurs assez puissants
à l'époque, constitue une vérification remarquable du pouvoir prédictif d'un
tel traitement théorique, et vérifie l'adéquation du formalisme aux phénomènes
à décrire...jusqu'à la prochaine remise en cause du cadre théorique par l'expérience !
|